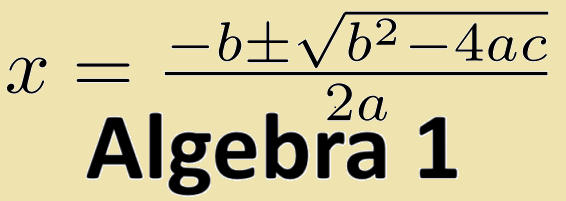Everything you Forgot About in Algebra 1

TABLE OF CONTENTS

• Introduction
• Mathematical Lexicon
  • What is a Number
  • Terminology
  • Symbols
  • Grouping
• The Rules
  • Operating with Signed Numbers
  • Dealing with Decimals and Fractions
  • Exponents
  • Roots
  • Order and Distribution
  • Factoring
• Solving Equations
  • Linear
  • Quadratics
  • Inequalities
  • Absolute Value
  • Word Problems
• Formulas
  • Introduction
  • Perimeter
  • Area
  • Volume
• Graphing
• Final Thoughts

Introduction

One day you are in high school 9th grade Algebra 1. You are sitting there solving for x, learning about lines, quadratics, and crazy things like imaginary numbers and radicals. Then you eventually graduate high school and move on with life. Then one day you have to remember this stuff again.

The following is a summary from Algebra 1 Essentials for Dummies to help you remember these math facts. I had to so I am hoping this will aid you in your journey of remembering to.

Mathematical Lexicon

What is a Number

• Real Numbers: are just what the name implies: real. Real numbers represent real values -- no pretend or make-believe. They cover the gamut and can take on any form -- fractions or whole numbers, decimal numbers, that go on forever and ever without end. positive or negatives.
• Natural Numbers: (also called counting number) is a number that comes naturally. The natural numbers are the numbers starting with 1 and going up by ones: 1, 2, 3, 4, 5, and so on into infinity.
• Whole Numbers: aren't a whole lot different from natural numbers. Whole numbers are just all the natural numbers plus a 0.
• Integer Numbers: Are positive and negative whole numbers. Integers are popular in algebra. When you solve a long, complicated problem and come up with an integer, you can be joyous because your answer is probably right. After all, most teachers like answers without fractions.
• Rational Numbers: is any number that can be written as a fraction, where the numerator and denominator are integers (except the denominator cannot be 0). If a number cannot be written as a fraction, then it isn't a rational number.
• Irrational Numbers: can't be written as a fraction and decimal values never end and never have the same, repeated pattern for them.
• Prime Numbers: if it can be divided evenly only by 1 and by itself.
• Composite Numbers: if it can be divided by at least one number other than 1 and itself.

Terminology

• Expression: any combination of values and operations that can be used to show how things belong together and compare to one another.
• Term: is a grouping together of one or more factors. Multiplication is the only thing connecting the number with the variables. Addition and subtraction on the other hand, separate terms from one another.
• Equation: Uses a sign to show a relationship -- that two things are equal.
• Operation: is an action performed upon one or two numbers to produce a resulting number. Operations are addition, subtraction, multiplication, division, square roots, and so on.
• Variable: is a letter representing some unknown; a variable always represents a number, but it varies until it's written in an equation or inequality.
• Constant: is a value or number that never changes in an equation -- it's constantly the same.
• Exponent: is a small number written slightly above and to the right of a variable or number. It's used to show repeated multiplication. An exponent is also called the power of the value.

Symbols

• + means add, find the sum, more than, or increased by; the result of addition is the sum. It is also used to indicate a positive number.
• - means subtract, minus, decreased by, or less than; the result is the difference. It's also used to indicate a negative number
• x means multiply or times. The values being multiplied together are the multipliers or factors. The result is the product. * or ⋅ may also be used. Typically it is not shown in an equation as it is implied multiplication with a number next to a variable or grouping symbols: ( ), , or
• ÷ means divide. The divisor divides the dividend. The result is the quotient. Other signs that indicate division are the fraction line and the slash /
• √ means to take the square root of something -- to find the number that, multiplied by itself, give you the number under the sign
• | | means to find the absolute value of a number, which is the number itself (if the number is positive) or its distance from 0 on the number line (if the number is negative)
• π is the Greek letter pi, which refers to the irrational number: 3.14159 . . . It represents the relationship between the diameter and circumference of a circle: π = C / d where C is the circumference and d is diameter
• ≈ means approximately equal or about equal. This symbol is useful when you're rounding a number

Grouping

• Parentheses ( ): are the most commonly used symbols for grouping
• Brackets and Braces : are also used frequently for grouping and have the same affect as parentheses. Utilized when multiple groups exist to help distinguish the order
• Radical √: Used for finding roots
• Fraction Line: also acts as a group symbol -- everything in the numerator (above the line) is group together, and everything in the denominator (below the line) is grouped together

The Rules

Operating with Signed Numbers

1. When the signs are the same, you find the sum and the sign of the sum is the same as the signs. This rule holds when a and b represent any two positive real numbers:

   • (+a) + (+b) = +(a + b)
   • (-a) + (-b) = -(a + b)

2. When the signs of two numbers are different, forget the signs for a while and find the difference between the numbers. This is the difference between their absolute values. The number farther from zero determines the sign of the answer:

   • (+a) + (-b) = +(|a| - |b|) if the positive a is farther from zero
   • (+a) + (-b) = -(|b| - |a|) if the negative b is farther from zero

3. When subtracting signed numbers, change the minus sign to a plus sign and change the number that the minus sign was in front of to its opposite. Then just add the numbers using the rules for adding signed numbers:

   • (+a) - (+b) = (+a) + (-b)
   • (+a) - (-b) = (+a) + (+b)
   • (-a) - (+b) = (-a) + (-b)
   • (-a) - (-b) = (-a) + (+b)

4. When multiplying and dividing two signed numbers, if the two signs are the same, then the result is positive; when the two signs are different, then the result is negative:

   • (+a) ⋅ (+b) = +ab
   • (+a) ÷ (+b) = +(a ÷ b)
   • (+a) ⋅ (-b) = -ab
   • (+a) ÷ (-b) = -(a ÷ b)
   • (-a) ⋅ (+b) = -ab
   • (-a) ÷ (+b) = -(a ÷ b)
   • (-a) ⋅ (-b) = +ab
   • (-a) ÷ (-b) = +(a ÷ b)

5. According to the even-odd rule, when multiplying and dividing a bunch of numbers, count the number of negatives to determine the final sign. An even number of negatives means the result is positive. An odd number of negatives means the result is negative.

Dealing with Decimals and Fractions

1. To change a fraction to a decimal, just divide the top by the bottom:

   • 7 / 4 becomes 4 厂 7.00 = 1.75, so 7 / 4 = 1.75
   • 4 / 11 becomes 11 厂 4.000000... = 0.363636... so the divisor never ends, so the three dots (ellipses) or bar across the top tell you that the pattern repeats forever.

2. To change a terminating decimal into a fraction, put the digits to the right of the decimal point in the numerator. Put the number 1 in the denominator followed by as many zeros as the numerator has digits. Reduce the fraction if necessary.

   • 0.36 = 36 / 100 = 9 / 25

3. To change a repeating decimal (in which every digit is part of the repeated pattern) into its corresponding fraction, write the repeating digits in the numerator of a fraction and, in the denominator, as many nines as there are repeating digits. Reduce the fraction if necessary

   • 0.126126126... = 126 / 999 = 14 / 111
   • 0.857142857142857142... = 857142 / 999999 = 6 / 7

Exponents

1. When a number x is involved in repeated multiplication of x times itself, then the number n can be used to describe how many multiplications are involved: xⁿ = x ⋅ x ⋅ x ⋅ x...n.

   • Even though the x in the expression xⁿ can be any real number and the n can be any real number, they can't both be 0 at the same time. For example, 0⁰ really has no meaning in algebra. Also, if x is equal to 0, then n can't be negative.
   • When the exponent is negative, you apply the rule involving rewriting negative exponents before writing the product.

2. To multiply powers of the same base, add the exponents together: x^a ⋅ x^b = x^a+b.

   • So 2⁴ ⋅ 2⁶ = 2⁴⁺⁶ = 2¹⁰
   • So a⁵ ⋅ a⁸ = a¹³

3. When there's no exponent showing, you assume that the exponent is 1. So if you see y + y³ it will translate to y¹ + y³ = y⁴.

4. To divide powers with the same base, subtract the exponents: x^a ÷ x^b = x^a-b, where x can be any real number except 0 (because you can't divide by 0).

   • 2¹⁰ ÷ 2⁴ = 2^10-4 = 2⁶
   • (4x⁶ ⋅ y³ ⋅ z²) / (2x⁴ ⋅ y³ ⋅ z) = 2^6-4 ⋅ y^3-3 ⋅ z^2-1 = 2x² ⋅ z

5. Any number to the power of 0 equals 1 as long as the base number is not 0. In other words, a⁰ = 1 as long as a ≠ 0

6. The reciprocal of x^a is 1 / x^a which can be rewritten as x^-a. The variable x is any real number except 0, and a is any real number. Also, to get rid of the negative exponent, you write x^-a = 1 / x^a

7. To raise a power to a power, use this formula: (xⁿ)^m = x^{n ⋅ m}. In other words, when the whole expression, xⁿ, is raised to the m power, the new power of x is determined by multiplying n and m together.

Roots

1. Expressions with radicals can be multiplied or divided as long as the root power or the value under the radical is the same. Expressions with radicals cannot be added or subtracted unless both the root power and the value under the radical are the same.

   • √2 ⋅ √3 = √6: These can be combined because it's multiplication, and the root power is the same.
   • √8 ÷ √4 = √2: These can be combined because it's division, and the root power is the same.
   • √2 + √3: These cannot be combined because it's addition, and the value under the radical is not the same.
   • 4√3 + 2√3 = 6√3: These can be combined because the root power and the numbers under the radical are the same

2. Here are the rules for adding, subtracting, multiplying, and dividing radical expressions. Assume that a and b are positive values.

   • m√a ± n√a = (m ± n)√a: Addition and subtraction can be performed if the root power and the value under the radical are the same.
   • √a ⋅ √a = √a² = |a|: The number a cannot be negative, so the absolute value insures a positive result
   • √a ⋅ √b = √(a ⋅ b) or √a ÷ √b = √(a / b): Multiplication and division can be performed if the root powers are the same

3. When changing from radical form to fractional form exponents:

   • ⁿ√a = a^1/n: The nth root of a can be written as a fractional exponent with a raised to the reciprocal of that power
   • ⁿ√a^m = a^m/n: When the nth root of a^m is taken, it's raised to the 1/n th power. Using the "powers of powers" rule, the m and the 1/n are multiplied together

Order and Distribution

1. According to the order of operations, work out the operations and signs in the following order:

   1. Powers and roots
   2. Multiplication and division
   3. Addition and subtraction

2. To distribute a term over several other terms, multiply each of the other terms by the first. Distribution is multiplying each individual term in a grouped series of terms by a value outside the grouping.

   • a(b + c + d + e + ...) = ab + ac + ad + ae + ...

3. When distributing a negative sign, each term has a change of sign: from negative to positive or from positive to negative.

4. When distributing a polynomial (many terms) over any number of other terms, multiply each term in the first factor times each term in the second factor. When the distribution is done, combine anything that goes together to simplify.

   • (a + b + c + d + ...)(z + y + w + ...) = az + ay +ax + aw + ... + bz + by + bx + bw + ... + cz + cy + cx + cw + ... + dz + dy + dx + dw + ...

Factoring

1. An expression can be written as the product of the largest number that divides all the terms evenly times the results of the divisions: ab + ac + ad = a(b + c + d). The absolutely proper way to factor an expression is to write the prime factorization of each of the numbers and look for the greatest common factor (GCF), which is the largest possible divisor shared by all the terms. What's really more practical and quicker in the end is to look for the biggest factor that you can easily recognize. Factor it out and then see if the numbers in the parentheses need to be factored again. Repeat the division until the terms in the parentheses are relatively prime.

2. When factoring out powers of a variable, the smallest power that appears in any one term is the most that can be factored out. For example, in an expression such as a⁴b + a³c + a²d + a³e⁴, the smallest power of a that appears in any term is the second power, a². So you can factor out a² from all terms because a² is the GCF. You can't factor anything else out of each term: a⁴b + a³c + a²d + a³e⁴ = a²(a²b + a¹1c + d + a¹e⁴)

3. The quadratic, or second-degree, expression in x has the x variable that is squared, and no x terms with powers higher than 2. The coefficient on the squared variable is not equal to 0. The standard quadratic form is ax² + bx + c. By convention, the terms are usually written with the second degree term first, the first degree term next, and the number last. After you find the variable that's squared, write the rest of the expression in decreasing powers of that variable.

4. FOIL is an acronym used to help multiply two binomials together by distribution. The F stands for first; O, for outer; I, for inner; and L, for last. Many quadratic expressions, such as 6x² + 7x - 3 are the result of multiplying two binomials (expressions with two terms), so you can undo the multiplication by factoring them.

   • 6x² + 7x - 3 = (2x + 3)(3x - 1)

5. Follow these steps to factor the quadratic ax² + bx + c, using unFOIL.

   1. Determine all the ways you can multiply two numbers to get a.
   2. Determine all the ways you can multiply two numbers together to get c.
   3. Now look at the sign of c and your lists from steps 1 and 2
      • If c is positive, find the value from your Step 1 list and another from your Step 2 list such that the sum of their product and the product of the two numbers they're paired with in those steps results in b
      • If c is negative, find a value from your Step 1 list and another from your Step 2 list such that the difference of their product and the product of the two numbers they're paired with from those steps results in b
   4. Arrange your choices as binomials
   5. Place the signs as appropriately.

6. Here are the four ways to factor a binomial:

   • Finding the GCF
   • Factoring the difference of two perfect squares
   • Factoring the difference of two perfect cubes
   • Factoring the sum of two perfect cubes

7. If subtraction separates two squared terms, then the product of the sum and difference of the two square roots factors the binomial: a² - b² = (a + b)(a - b)

8. To factor the difference of two perfect cubes, use the following pattern: a³ - b³ = (a - b)(a² + ab + b²)

9. To factor the sum of two perfect cubes, use the following pattern: a³ + b³ = (a + b)(a² - ab + b²)

10. The quadratic-like equation ax²ⁿ + bx² + c may factor into the product of two binomials in the form of (dxⁿ + e)(fxⁿ + g)

11. The remainder theorem states that the remainder, R, resulting from dividing P(x) = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₁x¹ + a₀ by x + a is equal to P(-a).

12. The rational root theorem says that if a rational number (a number that can be written as a fraction) is a solution, r, of the equation a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₁x¹ + a₀ = 0, then r = some factor of a₀ / some factor of a_n. Using the rational root theorem for my factoring, I just find these possible solutions of the equation and do the synthetic division using only these possibilities.

Solving Equations

Linear

1. When you're solving equations, you still usually deal with the grouping symbols first, but, for the rest of the equation, you reverse the order of operations:

   1. Do all the addition and subtraction. Combine all terms that can be combined both on the same side of the equation and on the opposite sides using addition and subtraction.
   2. Do all multiplication and division. This step is usually the one that isolates or solves for the value of the variable or some power of the variable.
   3. Multiply exponents and find the roots. Powers and roots aren't found in these linear equations -- they come in quadratic and higher powered equations. But these would come next in the reverse order of operations.

2. Given the proportions ^a⁄_b = ^c⁄_d:

   • The cross-products are equal: ad = bc
   • The reciprocals are equal: ^b⁄_a = ^d⁄_c
   • You can reduce the fractions vertically, as usual: ^{e ⋅ f}⁄_{e ⋅ g} = ^c⁄_d
   • You can reduce horizontally, across the equal sign:
     • ^{e ⋅ f}⁄_f = ^{e ⋅ g}⁄_d
     • ^a⁄_{e ⋅ f} = ^c⁄_{e ⋅ g}
   • When reducing proportions., you can divide vertically or horizontally, but you can't reduce the fractions diagonally. The diagonal reductions are done when you're multiplying fractions and you have a multiplication symbol between them, not an equal sign between them.

Quadratics

1. A quadratic equation has a general form that looks like this: ax² + bx + c = 0. The constants a, b, and c in the equation are real numbers, and a cannot be equal to 0. (f a were 0, you wouldn't have a quadratic equation anymore).

2. When b = 0, the equation will look like ax² + c = 0, but the c is usually negative, giving you ax² - c = 0, and the equation is rewritten as ax² = c.

3. If x² = k, then x = ± √k or if ax² = c, then x = ± √^c⁄_a. If the square of a variable is equal to the number k, then the variable is equal to either a positive or negative number -- both the positive and negative roots of k.

4. The multiplication property of zero (MPZ) states that if pq = 0, then either p = 0 or q = 0. One of them must be equal to 0 (or both could be 0).

5. The quadratic formula says that if an equation is in the form of ax² + bx + c = 0, then its solutions, the values of x, can be found with the following: x = -b ± √b² - 4ac / 2a. Sometimes using the quadratic formula is easier if the equation has really large or nasty numbers. In general, though, when you can, factoring using unFOIL and then the MPZ, is quicker. Things to watch out for

   • Don't forget that -b means to use the opposite of b. If the coefficient b in the standard form of the equation is a positive number, change it to a negative number before inserting into the formula. If b is negative, then change it to positive in the formula.
   • Be careful when simplifying under the radical. The order of operations dictates that you square the value of b first, and then multiply the last three factors together before subtracting them from the square of b. Some sign errors can occur if you're not careful.

6. The square root of -1 is designated as i. Therefore √-1 = i and i² = -1

Inequalities

1. Algebraic inequalities show relationships between a number an expression or between two expressions. The inequality relation is a bit less than precise. One thing can be bigger by a lot or bigger by a little, but there's still that relationship between them -- that one is bigger than the other. Many operations involving inequalities work the same as operations on equalities and equations, but you need to pay attention to some important differences.

2. The inequality symbology is as follows:

   • < Less than
   • > Greater than
   • ≤ Less than or equal to
   • ≥ Greater than or equal to

3. Interval notation expresses inequality statements with the following rules:

   • Parentheses to show less than or greater than (but no including)
   • Brackets to show less than or equal to or greater than or equal to
   • Parentheses at both infinity or negative infinity
   • Numbers and symbols written in the same left-to-right order as on a number line

4. Examples of Interval notation and Inequality statements are as follows:

   • -3 ≤ x ≤ 11 becomes [-3, 11]
   • -4 ≤ x < -3 becomes [-4, -3)
   • x > -9 becomes (-9, ∞)
   • [-8, 5] becomes -5 ≤ x ≤ 5
   • (-∞, 0] becomes x ≤ 0
   • (44, ∞) becomes x > 44

5. The rules for operations on inequalities are given here. The rules shown are for less than (<), but they also apply to greater than (>):

   • If a < b, then a + c < b + c and a - c < b - c. The direction of the inequality stays the same.
   • If a < b and c is positive, then a ⋅ c < b ⋅ c and ^a⁄_c < ^b⁄_c. The direction of the inequality stays the same.
   • If a < b and c is negative, then a ⋅ c > b ⋅ c and ^a⁄_c > ^b⁄_c. When multiplying or dividing with a negative number, the direction of the inequality symbol changes.
   • If ^a⁄_c < ^b⁄_d, then ^c⁄_a > ^d⁄_b. The inequality symbol changes when you flip (write the reciprocals of) the fraction.

Absolute Value

1. To solve an absolute-value equation of the form |ax + b| = c, change the absolute-value equation to two equivalent linear equations and solve for them. This is equivalent to:

   • ax + b = c
   • ax + b = -c

2. To solve an absolute-value inequality of the form |ax + b| > c, change the absolute-value inequality to two inequalities equivalent to tht original problem and solve them.

   • ax + b > c
   • ax + b < -c

3. To solve an absolute-value inequality of the form |ax + b| < c, change the absolute-value inequality to an equivalent compound inequality and solve it. The equivalent is -c < ax + b < c

Word Problems

1. When solving story problems, the equation you should use or how all the ingredients interact isn't always immediately apparent. It helps to have a game plan to get you started.

2. Draw a picture. Label your picture with numbers or names or other information that helps you make sense of the situation. Fill it in more or change the drawing as you set up an equation for the problem.

3. Assign a variable(s) to represent how many or number of. You may use more than one variable at first and refine the problem to just one variable later.

4. If you use more than one variable, go back and substitute known relationships for the extra variables. When it comes to solving the equations, you want to solve for just one variable. You can often rewrite all the variables in terms of just one of them.

5. Look at the end of the question or problem statement. This often gives a big clue as to what's being asked for and what the variable should represent. It can also give a clue as to what formula to use, if a formula is appropriate.

6. Translate the words into an equation. Replace:

   • and, more than, and exceeded by with the plus sign +
   • less than, less, and subtract from with the minus sign -
   • of and times as much with the multiplication sign x
   • twice with two times 2x
   • divided by with the division sign ÷
   • half as much with one-half times ¹⁄₂x
   • the verb (is or are, for example) with the equal sign =

7. Plug in a standard formula, if the problem lends itself to one. When possible, use a formula as your equation or as part of your equation. Formulas are a good place to start to setup relationships. Be familiar with what the variables in the formula stand for.

8. Check to see if the answer makes any sense. When you get an answer, decide whether it makes sense within the context of the problem. Having an answer make sense doesn't guarantee that it's a correct answer, but it is the first check to tell if it is not correct.

Formulas

Introduction

1. A formula is an equation that represents a relationship between some structures, quantities, or other entities. It's a rule that uses mathematical computations and can be counted on to be accurate each time you use it (when applied correctly). See the The Forgotten Mathematical Formulas article for details of all documented formulas.

2. The amount of simple interest earned is equal to the amount of the principal, P (the starting amount), times the rate of interest, r (which is written as a decimal), times the amount of time, t (usually in years). The formula to calculate simple interest is: I = Prt

3. The formula d = rt means the distance traveled is equal to the rate r (the speed) times the how long it takes, t (the time). Solving the formula for either the rate or the time, you get: r = ^d⁄_t and t = ^d⁄_r. Given any two of the values, you can solve for the third. You change the original formula to one that you can use. Always be sure that the units are the same: Miles per day and total number of miles go together, but miles per hour and total number of days would take some adjusting.

4. According to the Pythagorean theorem, if a, b, and c are the lengths of the sides of a right triangle, and c is the longest side (the hypotenuse), then a² + b² = c²

Perimeter

1. The perimeter of a triangle is equal to the sum of the measures of the three sides: P = s₁ + s₂ + s₃.

2. The perimeter of a square is four times the length of a side: P = 4s.

3. The perimeter of a rectangle is twice the length plus twice the width. Or you can add the length and width together and then multiply that sum by two. Translated: P = 2l + 2w = 2(l + w).

4. The formula for circumference (distance around the outside of a circle) is C = 2πr = πd where r is the radius, d is the diameter, and π is always about 3.14 or about ²²⁄₇.

Area

1. The area of a rectangle is its length times its width A = lw, and the area of a square is the square of the measure of any side A = s²

2. The area of a triangle is equal to half the product of the measure of the base of the triangle, b, times the height of the triangle, h, A = ¹⁄₂bh.

3. The formula for the area of a circle is π (about 3.14) times the radius squared: A = πr².

Volume

1. The formula for finding the volume of a prism is V = lwh, which means that the volume is equal to the product of the length, l, times the width, w, time the height, h.

2. The formula for the volume of a cylinder is V = πr²h. The volume is equal to π times the radius (halfway across a circle) squared times the height.

3. The formula for the volume of a pyramid is V = ¹⁄₃(area of base) ⋅ h.

4. The formula for the volume of a cone is V = ¹⁄₃πr²h.

Graphing

1. A straight line is the set of all the points on a graph that satisfy a linear equation. When any two points on a line are chosen, the slope of the segment between those two points is always the same number.

2. An equation whose graph is a straight line is said to be linear. A linear equation has a standard form of ax + by = c, where X and y are variables and a, b, and c are real numbers. A point (x, y) lies on the line if the x and y make the equation true. When graphing a line, you can find some pairs of numbers that make the equation true and then connect them. Connect the dots!

3. The x-intercept of a line is where the line crosses the x-axis. To find the x-intercept, let the y in the equation equal 0 and solve for x.

4. The y-intercept of a line is where the line crosses the y-axis. The fin the y-intercept, let the x in the equation equal 0 and solve for y.

5. The slope of a line, denoted by the small letter m, is found when you know the coordinates of two points on the line, (x₁, y₁) and (x₂, y₂): m = ^{y₂ - y₁}⁄_{x2 - x1}

6. Where y and x represent coordinates of a point on the line, m is the slope of the line, and b is the y-intercept of the line, the slop-intercept form is y = mx + b.

7. If l₁, has a slope of m₁ and if line l₂ has a slope of m₂, then the lines are parallel if m₁ = m₂. If line l₁ has a slope of m₁, and if line l₂ has a slope of m₂ then the lines are perpendicular if m₁ = - ¹⁄_m2 of if they are horizontal or vertical lines.

Final Thoughts

1. Including the middle term. A squared binomial has three terms in the answer. The term that often gets left out is the middle term. Right Way: (a + b)² = a² + 2ab + b².

2. Keeping distributions fair. Distributing a number or a negative sign over two or more terms in a parentheses can cause problems if you forget to distributes the outside value over every single term in the parentheses. Right Way: x - 2(y + z - w) = x - 2y - 2z + 2w

3. Creating two fractions from one. Splitting a fraction into several smaller pieces is all right as long as each piece has a term from the numerator (top) and the entire denominator (bottom). You can't split up the denominator. Right Way: ^{x + y}⁄_{a + b} = ^x⁄_{a + b} + ^y⁄_{a + b}

4. Restructuring Radicals. Only multiplied or divided radicals under a root can be split up into separate radicals. You can't split addition or subtraction.

5. Including the negative or not. The oder of operations instructs you to raise the expression to a power before you add or subtract. A negative in front of a term acts the same as subtracting, so the subtracting has to be done last. Right Way: -3² = -9 or (-3)² = 9.

6. Making exponents fractional. A fractional exponent has the power on the top of the fraction and the root on the bottom. Right Way: ⁵√(x³) = x^3⁄₅

7. Keeping bases the same. When you are multiplying numbers with exponents, and those numbers have the same base, you add the exponents and leave the base as it is. The bases never get multiplied together.

8. Powering up a power. To raise a value that has a power (exponent) to another power, multiply the exponents to raise the whole term to a new power. Don't raise the exponent itself to a power -- it's the base that's being raised, not the exponent. Right Way: (x²)⁴ = x⁸.

9. Making reasonable reductions. When reducing fractions with a numerator that has more than one term separated by addition or subtraction, then whatever you're reducing the fraction by has to dividing every single term evenly in both the numerator and the denominator. Right Way: ^{(4 + 6x)}⁄₄ = ^{(2 + 3x)}⁄₂.

10. Catching all the negative exponents. When changing fractions to equivalent expressions with negative exponents, give every single factor in the denominator a negative exponent.